1. 퍼셉트론이란?

퍼셉트론은 프랑크 로젠블라트(Frank Rosenblatt)가 1975년에 고안한 알고리즘으로 신경망(딥러닝)의 기원이 되는 알고리즘이다. 퍼셉트론은 다수의 신호를 입력으로 받아서 하나의 신호를 출력하는 방식으로 흐른다/흐르지 않는다 (1이나 0)중에 하나를 출력한다. 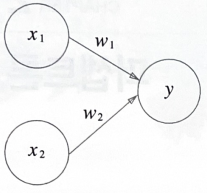입력이 2개인 퍼셉트론 2개의 신호를 받는 퍼셉트론의 예
위의 그림에서 x1과x2는 입력신호, y는 출력신호, w1과w2는 가중치를 뜻한다. 여기서 원을 노드 또는 뉴런이라고 한다. 입력신호를 뉴런에 보낼때 입력신호에 가중치를 곱하는데 뉴런에서 보내온 신호의 총 합이 임계값 θ를 넘을 때에 1을 출력한다.
이를 수식으로 나타내면 다음과 같다. 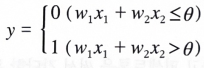입력이 2개인 퍼셉트론 수식 이와같이 퍼셉트론은 입력신호 각각에 가중치를 곱하여 뉴런으로 보내는데 여기서 가중치란 각 신호가 결과의 미치는 영향력이라고 할 수 있다.

2. 퍼셉트론 구현하기

2.1 간단한 구현

처음에는 간단한 AND함수를 퍼셉트론으로 구현해보았다.

  
def AND(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7
    tmp = x1*w1 + x2*w2
    if tmp <= theta:
        return 0
    elif tmp > theta:
        return 1

  
print(AND(0,0)) # 0
print(AND(1,0)) # 0
print(AND(0,1)) # 0
print(AND(1,1)) # 1

이렇게 예상한 대로 작동하는것을 확인하였다.

2.2 가중치와 편향 도입

위에서 퍼셉트론을 수식으로 나타냇지만 이를 약간 수정하고자 한다. 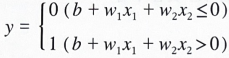편향이 도입된 퍼셉트론 위의 수식과 비교해보자면 단순히 기호표기만 바꿧을 뿐, 그 의미는 동일하며 b를 편향이라고 하고 w1과w2는 그대로 가중치이다.

2.3 가중치와 편향 구현

위의 가중치와 편향이 도입된 식을 numpy를 사용해서 구현하였다.

  
import numpy as np
def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

이렇게 처음의 식과 비교하면 -θ가 b로 치환되었고 numpy를 이용하여 행렬연산을 수행하는 것을 알수있다.
가중치와 편향을 혼동할 수도 있는데 여기서 가중치(w1,w2)는 각 입력신호가 결과에 주는 영향력(중요도)을 조절하는 매개변수이고 편향(b)는 뉴런이 얼마나 쉽게 활성화(결과로 1을 출력)하느냐를 조정하는 매개변수이다.
이 퍼셉트론을 이용해 AND게이트 이외에도 NAND, OR게이트 등등을 구현할 수 있다.

3. 퍼셉트론의 한계

3.1 XOR게이트 구현하기?

방금 위에서 AND회로를 퍼셉트론으로 구현하였다. 그렇다면 XOR게이트도 퍼셉트론으로 구현할수 있을까?
XOR게이트의 진리표는 다음과 같다. 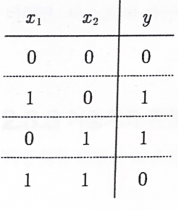XOR게이트 진리표 사실 XOR게이트는 지금까지 본 퍼셉트론으로는 구현할 수 없다. 그 이유가 뭘까?
그 이유는 그림으로 그려보면 쉽게 알 수 있는데 OR게이트의 가중치 매개변수가 (b,w1,w2) = (0.5, 1.0, 1.0)인 퍼셉트론을 생각해 보자. 이때의 퍼셉트론은 다음과 같이 표시된다. 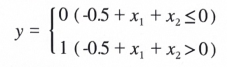OR게이트 퍼셉트론 수식 퍼셉트론은 직선으로 나뉜 두 영역을 만드는데 이를 그림으로 나타내 보면 다음과 같다. 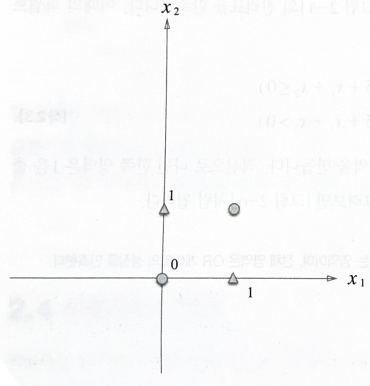OR게이트 퍼셉트론 시각화 이렇게 이 그림의 직선은 네 점을 제대로 나누고 있음을 알 수 있다. 그럼 XOR게이트의 경우는 어떨까? XOR게이트 퍼셉트론 시각화 이렇게 XOR게이트의 경우에는 직선 하나로 나누기는 불가능하다 ##. 3.2 선형과 비선형 직선하나로는 ○와△를 나눌 수 없지만 곡선이라면 가능하다. 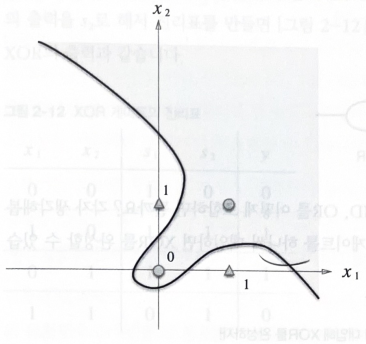XOR게이트 퍼셉트론 시각화 (곡선) 퍼셉트론은 직선 하나로 나눈 영역만 표현할 수 있다는 한계가 있다.
참고로 방금과 같은 곡선의 영역을 비선형영역, 직선의 영역을 선형영역 이라고 하고 기계학습분야에서 자주 쓰이는 용어이다.

4. 다층 퍼셉트론

위에서 본것과 같이 단층 퍼셉트론으로는 XOR게이트를 표현할 수 없지만, 사실 퍼셉트론은 ‘층을 쌓아’ 다층 퍼셉트론(multi-layer perceptron)을 만들 수 있다.

4.1 게이트 조합하여 XOR게이트 만들기

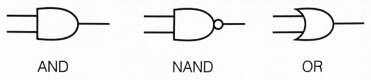
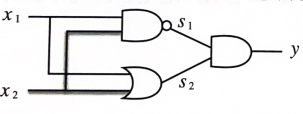게이트 기호 이와 같이 AND, NAND, OR게이트들을 조합하여 XOR게이트를 만들 수 있다는 것을 알았다.

4.2 XOR게이트 구현

그럼 이를 실제로 구현해 보자.

  
def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

  
print(XOR(0,0)) # 0
print(XOR(1,0)) # 1
print(XOR(0,1)) # 1
print(XOR(1,1)) # 0

이와 같이 XOR게이트를 구현할수 있다. 그리고 이를 뉴런을 이용한 퍼셉트론으로 표현하면 다음과 같이 된다. 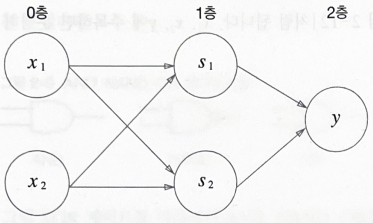XOR 퍼셉트론 이렇게 퍼셉트론의 층을 늘려서 2층구조를 사용해 XOR게이트를 표현할 수 있었다. 다시말해 단층 퍼셉트론으로는 표현하지 못한 것을 층을 하나 늘려 구현할 수 있다는 뜻이다. 이렇게 퍼셉트론은 층을 쌓아(깊게 하여) 더 다양한 것을 표현할 수 있다.
예를 들면 가산기, 인코더 부터 시작해서 더 나아가 컴퓨터까지도 표현할 수 있다!
이것이 가능한 이유는 NAND게이트 만으로 컴퓨터를 만들 수 있는데 퍼셉트론으로 NAND게이트를 만들 수 있기 때문에 이는 퍼셉트론으로 컴퓨터를 표현할 수 있다는 사실로 이어진다.

5. 정리

퍼셉트론은 간단한 알고리즘이라 그 구조를 쉽게 이해할 수 있다. 그리고 이는 다음에 공부할 신경망의 기초가 된다.

퍼셉트론은 입출력을 갖춘 알고리즘이다. 입력을 주면 정해진 규칙에 따른 값을 출력한다.
퍼셉트론에서는 ‘가중치’와 편향’을 매개변수로 설정한다.
퍼셉트론으로 AND, OR게이트 등의 논리 회로를 표현할 수 있다.
XOR 게이트는 단층 퍼셉트론으로는 표현할 수 없다.
2층 퍼셉트론을 이용하면 XOR게이트를 표현할 수 있다.
단층 퍼셉트론은 직선형 영역만 표현할 수 있고, 다층 퍼셉트론은 비선형 영역도 표현할 수 있다.
다층 퍼셉트론은 (이론상) 컴퓨터를 표현할 수 있다.

딥러닝 개발일지[1] - 퍼셉트론(Perceptron)